算法与数据结构(树)
算法与数据结构  0次访问

算法与数据结构(树)

由于页面比较长，即时的使用回到右下角的“回到顶部”按钮可以很方便的回到最前面查看目录。

——以下题目均来自于PAT甲级题库。

1004.Counting Leaves (30分)(树的遍历)

思路
这里使用了数组模拟邻接表来进行数的存储，把存一棵树当成存一个有向图即可。这题只用不断的遍历结点的子节点，然后找出叶子节点即可，即h[u]=-1的点。

代码

Counting Leaves
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/*
类似于图的遍历;
即存一个有向图，边的指向为父节点到字节点；
*/

#include<iostream>
#include<cstring>
using namespace std;

const int N=110;
int h[N],e[N],ne[N],idx;
int cnt[N];//记录每层的叶子节点
int max_depth;//记录的是当前最大的深度
int n,m;
void add(int a,int b){
    e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}

//u:当前遍历到的结点   depth:当前的深度
void dfs(int u,int depth){
    if(h[u]==-1){
        max_depth=max(depth,max_depth);
        cnt[depth]++;
        return;
    }
    //遍历u的儿子
    for(int i=h[u];~i;i=ne[i])
        dfs(e[i],depth+1);
}

int main(){
    cin>>n>>m;
    memset(h,-1,sizeof h);
    for(int i=0;i<m;i++){
        int a,k,b;
        cin>>a>>k;
        for(int j=0;j<k;j++){
            cin>>b;
            //增加一条从a——>b的边；
            add(a,b);
        }
    }
    //一般根节点为第0层
    dfs(1,0);
    for(int i=0;i<=max_depth;i++){
        if(i!=0) cout<<" ";
        cout<<cnt[i];
    }


    return 0;
}

1020.Tree Traversals (25分)(树的遍历)

思路

给定一棵树的前序遍历和中序遍历或者后序遍历和中序遍历，则可以唯一的确定一棵树。

思路
该题给定了树的后序遍历(postorder sequence)和中序遍历(inorder sequence)然后让我们输出树的层序遍历。显然我们应该先把这棵树给确定下来,建树的步骤:
  1. 首先我们可以根据后序遍历来确定根节点，后序序列的最后一个元素即为树的根节点x。
  2. 然后在中序序列中找到根节点`x`(这里可以用一个hash表来存每个值在中序遍历中的位置，这样会快一些！)，那么`x`左边的即为中序遍历下的左子树(左子树假设有`a`个结点)，右边的为右子树(右子树假设有`b`个结点)。
  3. 后序序列的前`a`个结点就是后序遍历下的左子树，而接着的`b`个结点就是后序遍历下的右子树。
  4. 由于现在已经确定了左右子树的中序遍历和后序遍历，那么继续像1~3那样去处理左右子树的后序和中序序列，递归下去即可确定整颗树！

注意这题的存图的方式我们直接用map来记录某个结点的左右子树即可这样比较方便！

代码

Tree Traversals
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<iostream>
#include<map>
#include<algorithm>
using namespace std;

const int N=40;
int postorder[N],inorder[N];
int q[N];//层次遍历用的队列
map<int,int> l,r,pos;//左孩子；右孩子；中序序列元素对应的下标（方便找出中序序列根节点）
int n;

//当前树所在的后序，中序序列的范围
int build(int il,int ir,int pl,int pr){
    int root = postorder[pr];//得到当前树的根节点（拿后序序列的最后一个元素）
    int k = pos[root];//得到在中序序列中k的下标（进行左右子树的划分）
    //存在左子树
    //中序和后序的长度一致；因此计算后序的右边界的时候可以根据 pl+中序长度 来确定
    if(il<k) l[root] = build(il,k-1,pl,pl+k-1-il);//得到当前节点的左孩子
    //存在右子树
    //这里后序遍历右子树的左端点根据左子树的右端点+1决定
    if(k<ir) r[root] = build(k+1,ir,pl+k-il,pr-1);
    return root;
}

void bfs(int root){
    int tt=-1,hh=0;
    q[++tt]=root;
    while(hh<=tt){
        int p=q[hh++];
        //该节点是否有左孩子
        if(l.count(p)) q[++tt] = l[p];
        if(r.count(p)) q[++tt] = r[p];
    }
    for(int i=0;i<=tt;i++){
        if(i!=0) cout<<" ";
        cout<<q[i];
    }
}

int main(){
    cin>>n;
    for(int i=0;i<n;i++) cin>>postorder[i];
    for(int i=0;i<n;i++){
        cin>>inorder[i];
        pos[inorder[i]]=i;
    }
    int root = build(0,n-1,0,n-1);
    bfs(root);
    return 0;
}

1021 Deepest Root (25分) (并查集+树的遍历)

思路
这题需要注意的是，可能给出的图不是一颗树，n个顶点,n-1条边，如果没有构成树，那么就只可能是存在环了，这样就可能会存在多个连通分量，因此这里很快可以想到，求解连通分量最简洁的做法就是并查集了。 如果该图是一棵树那么我们就要求解最大深度了，然后由于这题的时间限制比较宽裕，我们完全可以遍历每一个顶点，让它做一次根节点看看得到的最大深度是多少即可。还需要注意的是，我们这里存图要存的是无向图,因此在dfs遍历的时候要注意我们一定是朝一个方向遍历的而不能回去，因此每次dfs的时候要传递一个father变量表明是从哪个节点过来的。

代码

Deepest Root
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;

const int N = 1e4+10,M=2*N;
int p[N];
int h[N],e[M],ne[M],idx;
int n;
void add(int a,int b){
    e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}

int find(int x){
    if(x!=p[x]) p[x]=find(p[x]);
    return p[x];
}

int dfs(int u,int father){
    int depth=0;
    for(int i=h[u];~i;i=ne[i]){
        if(e[i]!=father)
            depth=max(depth,dfs(e[i],u)+1);
    }
    return depth;

}

int main(){
    cin>>n;
    //用cnt来记录当前还剩余的连通块数目，每合并一次连通块就少一个
    int cnt=n;
    memset(h,-1,sizeof h);
    for(int i=1;i<=n;i++) p[i]=i;
    
    for(int i=0;i<n-1;i++){
        int a,b;
        cin>>a>>b;
        int pa=find(a),pb=find(b);
        if(pa!=pb){
            p[pa]=pb;
            cnt--;
        }
        add(a,b);add(b,a);
    }
    if(cnt>1)
        printf("Error: %d components",cnt);
    else{
        int max_depth=0;
        vector<int> res;
        for(int i=1;i<=n;i++){
            int depth=dfs(i,-1);
            //以i为根节点得到的深度比max_depth大的话，那么之前res中记录的深度值都不可能成为最大值，那么都要删除
            if(depth>max_depth){
                max_depth=depth;
                res.clear();
                res.push_back(i);
            }else if(depth==max_depth) res.push_back(i);
        }
        for(auto ans:res){
            cout<<ans<<endl;
        }
    }
    return 0;
}

1043.Is It a Binary Search Tree (25分)(BST+树的遍历)

BST的定义:

  • 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值
  • 若它的右子树不空，则右子树上所有结点的值均大于或 等于 它的根结点的值
  • 它的左、右子树也分别为二叉搜索树
思路
  • 由上面的定义可以知道，BST的中序遍历一定是有序的，其顺序按照从小到大排布。因此拿到一个BST的前序遍历之后只要sort一遍就可以得到BST的中序遍历了。这样题目就变成给我们前序遍历和中序遍历，然后看我们是否可以构造出这棵树如果能则输出后序遍历的问题了(这里根据前序和中序构造一棵树和上面介绍的根据后序和中序构造一棵树很相似，这里只不过前序中根节点在开头，然后根节点后面的才接着是左子树和右子树，注意好这点即可)。还需注意的是由于这题中结点的值并不唯一，可能存在多个值相同的根节点，由于BST是右子树存在等于根节点的值，那么在中序中找根节点的时候在不同的值中找第一个即可。
  • BST的镜像即把BST的左右子树对调即可，可以发现其中序遍历刚好和上面的BST的中序遍历相反，它是从大到小排布的。同样的对于镜像BST我们就应该在不同元素中找最后一个！

    • 代码

    Is It a Binary Search Tree
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    #include<iostream>
    #include<algorithm>
    using namespace std;

    const int N = 1010;
    int postord[N],inord[N],preord[N];
    int n;

    int cnt=0;
    //中序左,右端点；前序左右端点；是否镜像
    bool build(int il,int ir,int pl,int pr,int type){
        int root=preord[pl];//前序首元素即为根节点
        int k;//找中序里面根节点的位置
        if(type==0){//BST中序中根节点的位置
            for(k=il;k<=ir;k++)
                if(root==inord[k]) break;
            if(k>ir) return false;
        }else{
            for(k=ir;k>=il;k--)
                if(root==inord[k]) break;
            if(k<il) return false;
        }
        bool res=true;
        //左
        if(k>il) res=res&build(il,k-1,pl+1,pl+1+(k-1-il),type);
        //右
        if(k<ir) res=res&build(k+1,ir,pl+1+(k-il),pl+1+(k-il)+(ir-k-1),type);
        //根
        postord[cnt++]=root;//给后序遍历赋值
        return res;
    }

    int main(){
        cin>>n;
        for(int i=0;i<n;i++){
            scanf("%d",&preord[i]);
            inord[i]=preord[i];
        } 
        
        sort(inord,inord+n);//BST中序
        
        if(build(0,n-1,0,n-1,0)){
            puts("YES");
            cout<<postord[0];
            for(int i=1;i<n;i++) cout<<" "<<postord[i];
        }else{
            reverse(inord,inord+n);//得到镜像BST中序
            cnt=0;//注意这里要还原cnt
            if(build(0,n-1,0,n-1,1)){
                puts("YES");
                cout<<postord[0];
                for(int i=1;i<n;i++) cout<<" "<<postord[i];
            }else puts("NO");
            
        }
        
        return 0;
    }

    1064.Complete Binary Search Tree (30分) (BST+完全二叉树)

    思路
    完全二叉树有很不错的性质，即我们可以只用一个数组就可以存完全二叉树了。假如把完全二叉树的层序遍历写出来的话我们可以发现有这样的规律：
    如果父亲结点的下标为x，左儿子的下标为a，右儿子的下标为b,则有： $$ a = x \times 2 ; b = x \times 2 + 1 ;$$ $$ x = \left \lfloor \frac{a}{2}\right\rfloor = \left \lfloor \frac{b}{2} \right \rfloor$$ 注意这里把树存到数组中下标要从1开始！
    由于让我们得到一棵完全二叉搜索树，我们已经知道BST满足其中序遍历递增的性质，因此这道题的步骤是:
  • 将给定的结点从小到大排序，再按中序遍历的顺序填到一棵完全二叉树中，这里就是按照中序顺序填到一个数组中即可。

    • 代码

    Complete Binary Search Tree
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    #include<iostream>
    #include<algorithm>
    using namespace std;
    const int N = 1010;
    int a[N],w[N];
    int n;
    void dfs(int u,int &k){//中序遍历
        //前
        if(2*u<=n) dfs(2*u,k);
        //中
        a[u]=w[k++];
        //后
        if(2*u+1<=n) dfs(2*u+1,k);
    }

    int main(){
        scanf("%d",&n);
        for(int i=0;i<n;i++) cin>>w[i];//由于w要sort所以i从0开始
        sort(w,w+n);//得到BST的中序遍历
        int k=0;
        dfs(1,k);//把BST填写到满二叉树中
        cout<<a[1];//注意用数组存二叉树的时候下标要从1开始，如果从0开始，
        //那么由左儿子公式2x可以得到会一直得0死循环
        for(int i=2;i<=n;i++)
            cout<<" "<<a[i];
        return 0;
    }

    1086.Tree Traversals Again (25分)二叉树的遍历

    思路
    这一题我们需要发现其中的规律:
  • 第一个被push进栈的是根节点
  • 在push的时候，如果上一个操作是push那么当前节点是上一个元素左儿子，如果上一个操作是pop那么当前节点是上一个元素的右儿子。

    • 代码

    Tree Traversals Again
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    #include<iostream>
    #include<map>
    #include<algorithm>
    #include<stack>
    using namespace std;
    map<int,int> l,r;//二叉树可以用map来保存某个结点的左右子树
    int n;
    int cnt;

    //后序遍历
    void dfs(int u){
        if(l.count(u)) dfs(l[u]);
        if(r.count(u)) dfs(r[u]);
        if(cnt) cout<<" ";
        cout<<u;
        cnt++;
    }

    int main(){
        cin>>n;
        stack<int> s;
        int last=0;//上一个被操作的结点
        int type;//上一个被操作结点的类型(push还是pop)
        int root;
        for(int i=0;i<2*n;i++){
            string op;
            cin>>op;
            
            if(op=="Push"){
                int x;
                cin>>x;
                if(last){
                    if(!type) l[last]=x;
                    else r[last]=x;
                }else root=x;//如果是第一次入栈那么它就是根节点
                last=x;
                type=0;//push
                s.push(x);
            }else{
                last=s.top();
                s.pop();
                type=1;//pop
            }
        }
        
        dfs(root);
        
        return 0;
    }

    1099.Build A Binary Search Tree (30分)(BST+树的遍历)

    思路
    这道题的意思就是说给了我们一颗二叉树，再给了我们一堆数据，然后让我们把数据往二叉树里面填，然后得到一棵BST。 因此我们可以用之前存二叉树的方式(map)，先把对应的二叉树的结构给存下来，然后读入要填的数据，把它sort一下，然后中序遍历刚刚的二叉树顺便把数据填进去(BST的性质)。之后层序遍历输出即可。

    代码

    Build A Binary Search Tree 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    #include<iostream>
    #include<map>
    #include<algorithm>

    using namespace std;

    map<int,int> l,r,w;//l,r存的是节点的左右儿子，w存的是节点的数值
    const int N = 110;
    int inord[N];
    int n;
    int cnt;
    //建树
    void dfs(int u){
        if(l[u]!=-1) dfs(l[u]);
        w[u]=inord[cnt++];
        if(r[u]!=-1) dfs(r[u]);
            
    }
    int q[N],tt=-1,hh=0;
    //层序遍历
    void level(int u){
        q[++tt]=u;
        cnt=0;
        while(hh<=tt){
            int t=q[hh++];
            if(cnt) cout<<" ";
            cout<<w[t];
            cnt++;
            if(l[t]!=-1) q[++tt]=l[t];
            if(r[t]!=-1) q[++tt]=r[t];
        }
    }

    int main(){
        cin>>n;
        for(int i=0;i<n;i++){
            int a,b;
            cin>>a>>b;
            l[i]=a;r[i]=b;
        }
        
        for(int i=0;i<n;i++) cin>>inord[i];
        //BST的中序遍历满足从小到大的性质
        sort(inord,inord+n);
        
        dfs(0);
        level(0);
        return 0;
    }

    1102.Invert a Binary Tree (25分)(二叉树的遍历)

    思路
    反转一颗二叉树也就是要得到一颗二叉树的镜像，我们只用在遍历二叉树的时候交换二叉树的左右结点即可，这样就达到了镜像的目的。然后再层序遍历，中序遍历一遍即可。

    代码

    Invert a Binary Tree
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    #include<iostream>
    #include<cstring>
    #include<algorithm>
    using namespace std;

    const int N = 12;
    int l[N],r[N];
    bool p[N];
    int q[N],tt=-1,hh=0;
    int n;
    //反转二叉树就是把二叉树的左右儿子进行交换
    void reverse(int u){
        if(u==-1) return;
        reverse(l[u]);
        reverse(r[u]);
        swap(l[u],r[u]);
    }

    void bfs(int u){
        q[++tt]=u;
        int cnt=0;
        while(hh<=tt){
            int t=q[hh++];
            if(cnt++) cout<<" ";
            cout<<t;
            if(l[t]!=-1) q[++tt]=l[t];
            if(r[t]!=-1) q[++tt]=r[t];
        }
        puts("");
    }

    void dfs(int u,int &k){
        if(l[u]!=-1) dfs(l[u],k);
        if(k++) cout<<" ";
        cout<<u;
        if(r[u]!=-1) dfs(r[u],k);
    }

    int main(){
        cin>>n;
        memset(l,-1,sizeof l);
        memset(r,-1,sizeof r);
        for(int i=0;i<n;i++){
            char a,b;
            cin>>a>>b;
            if(a!='-'){
                l[i]=a-'0';
                p[l[i]]=true;//由于i结点有左孩子l[i]同理l[i]也有父节点i
            } 
            if(b!='-'){
                r[i]=b-'0';
                p[r[i]]=true;
            } 
        }
        
        //没有父节点的结点就是根节点
        int root=0;
        while(p[root]) root++;
        
        //其实可以这样简单的交换即可无需遍历的时候交换
        for(int i=0;i<n;i++)
            swap(l[i],r[i]);
        
        //reverse(root);
        bfs(root);
        int k=0;
        dfs(root,k);
        
        
        return 0;
    }

    1110.Complete Binary Tree(25分)(完全二叉树的性质)

    思路
    这一题我们运用了完全二叉树的性质，即完全二叉树的层序遍历可以存到一个数组中，因此我们只用按照Complete Binary Search Tree中介绍的公式，从把根节点填到1号开始依次把左儿子填到2，右儿子填到3。。。这样不断的递归遍历下去按照规则把结点填到相应位置。当然这里我们没有必要真的开一个数组来存放结果，我们只用记录一下最后一个结点(号最大的那个)最终要填在数组中的位置即可，如果恰好等于n那么就是完全二叉树否则不是。

    代码

    Complete Binary Tree
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    #include<iostream>
    #include<cstring>

    using namespace std;

    const int N = 25;

    int l[N],r[N],tr[N];

    int max_id,max_k;//二叉树最后一个结点的编号，二叉树最后一个结点在数组中的下标
    int n;
    bool father[N];
    //二叉树结点编号;二叉树结点在数组中存储的下标
    void dfs(int u,int k){
        if(u==-1) return;
        if(k>max_k){//记录最后一个下标在数组中所存的值
            max_k=k;
            max_id=u;//由于需要输出id，因此要保存下
        }
        dfs(l[u],2*k);
        dfs(r[u],2*k+1);
    }

    int main(){
        cin>>n;
        memset(l,-1,sizeof l);
        memset(r,-1,sizeof r);
        for(int i=0;i<n;i++){
            string a,b;
            cin>>a>>b;
            if(a!="-"){
                l[i]=stoi(a);//把字符串转换为数字；同理itos()是把数字转换为字符串
                father[l[i]]=true;
            }
            if(b!="-"){
                r[i]=stoi(b);
                father[r[i]]=true;
            }
        }
        
        int root=0;
        while(father[root]) root++;
        
        dfs(root,1);
        //如果树里面最后一个元素存在数组中下标==n那么说明是可以用一个数组来存二叉树的，那么它是完全二叉树
        if(max_k==n) cout<<"YES "<<max_id;
        else cout<<"NO "<<root;
        return 0;
    }

    1115.Counting Nodes in a BST (30分)(BST的构建)

    思路
    这题是要求我们根据给定的这些数据的顺序，依次的插入到一棵树中，使其成为一颗BST。插入的思路大概是:
  • 递归的进行插入，如果当前的结点还没有插入过结点就把值填上去；
  • 如果当前要插入的值>=当前结点的值则递归到左子树中进行插入;
  • 如果当前要插入的值<当前结点的值则递归到右子树中进行插入。
    • 构建好BST之后再dfs一遍，把每层的结点数记录下即可。

    代码

    Counting Nodes in a BST 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    #include<iostream>
    #include<cstring>
    using namespace std;

    const int N = 1010;
    int l[N],r[N],w[N],cnt[N];
    int idx,n;
    int insert(int &u,int x){
        if(!u){
            u=++idx;//当u还没有填值的时候给u一个值,由于u是引入的形式传入，在这里修改之后
            //传入的位置也会得到修改
            w[u]=x;
        }else if(x<=w[u]) insert(l[u],x);//注意这题定义的是<=的放在左边
        else if(x>w[u]) insert(r[u],x);
    }
    int max_depth;
    void dfs(int u,int depth){
        if(!u) return;
        max_depth=max(max_depth,depth);
        cnt[depth]++;
        dfs(l[u],depth+1);
        dfs(r[u],depth+1);
    }

    int main(){
        cin>>n;
        int root=0;
        for(int i=0;i<n;i++){
            int x;
            cin>>x;
            insert(root,x);
        }
        dfs(root,0);
        int res=cnt[max_depth]+cnt[max_depth-1];
        printf("%d + %d = %d",cnt[max_depth],cnt[max_depth-1],res);
        return 0;
    }

    🐲1119.Pre- and Post-order Traversals (30分) (树的遍历)

    思路
    我们知道只根据前序遍历和后序遍历是无法唯一确定一棵树的，给了我们这两个序列我们只能确定根节点在哪里，但是左右子树从哪里分开是很难确定的，因此由于此题的数据量比较小，我们可以使用暴力枚举的方法，即我们枚举左子树的长度，这样剩下的就是右子树的长度，这样就可以分出左右子树了，让后再递归下去，再这样枚举左子树的长度，划分左右子树后，再递归一层枚举左子树的长度，划分好左右子树。。。显然这样的做法的时间复杂度是阶乘级别的，但是并不是随便划分一下长度都可以满足条件的，因为要想这样划分左右子树成立，必须前序的最开头的结点和后序最结尾的结点必须是相等的，因为这两个结点都代表着根节点，因此仅根据这个都可以淘汰掉很大一部分情况。

    代码

    Pre- and Post-order Traversals 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    #include<iostream>
    #include<string>
    #include<algorithm>
    using namespace std;

    const int N = 40;
    int pre[N],post[N];
    int n;

    int dfs(int prel,int prer,int postl,int postr,string &s){
        if(prel>prer) return 1;//空树算一种情况；这里只用考虑前序即可，因为相同的子树在后序上数量是相等的
        if(pre[prel]!=post[postr]) return 0;//如果前序的右端(根)和后序的左端(根)不相等则代表构建子树失败
        int cnt=0;
        //枚举左子树的长度，右子树就是另一半
        for(int i=prel;i<=prer;i++){
            string spre,spost;
            int cntl=dfs(prel+1,i,postl,postl+i-prel-1,spre);//枚举左子树
            int cntr=dfs(i+1,prer,postl+i-prel,postr-1,spost);//枚举右子树
            
            if(cntl&&cntr){
                /*根据递归的特性，递归会一直递归到最底层之后才会返回，因此只有当子树只剩下一个结点的时候才会返回
                这样的话显然左右子树就是空那么返回的形式就是<单个结点+空格>,所以返回的时候把这些东西拼起来的话，
                由于单个字符右边有空格所以左子树右边自带空格是不需要再加多余空格的，由于右子树也有空格所以最后产生的字符串
                会在末尾多一个空格，在最终输出的时候记得要删除这个空格*/
                s=spre + to_string(pre[prel])+" "+spost;
                cnt+=cntl*cntr;
                if(cnt>1) return cnt;
            }
        }
        return cnt;
    }

    int main(){
        cin>>n;
        for(int i=0;i<n;i++) cin>>pre[i];
        for(int i=0;i<n;i++) cin>>post[i];
        string s;
        int cnt=dfs(0,n-1,0,n-1,s);
        if(cnt>1) puts("No");
        else puts("Yes");
        s.pop_back();
        //注意这里要输出换行符，我也不知道为啥o(╥﹏╥)o
        cout<<s<<endl;
        
        
        return 0;
    }

    1127.ZigZagging on a Tree (30分)(二叉树的建立+层序遍历)

    思路
    首先我们根据后序序列和中序序列建树，然后层序遍历树，需要注意的是，对于奇数层的结点我们要从右往左输出，因此我们在层序遍历的时候把奇数层的序列反转一下即可。

    代码

    ZigZagging on a Tree
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    #include<iostream>
    #include<map>
    #include<algorithm>
    using namespace std;

    const int N = 40;

    map<int,int> l,r,pos;
    int level[N],inord[N],post[N];
    int n;

    //中序+后序建树
    int build(int il,int ir,int pl,int pr){
        int root=post[pr];
        int k=pos[root];
        
        if(k>il) l[root]=build(il,k-1,pl,pl+k-1-il);
        if(k<ir) r[root]=build(k+1,ir,pl+k-1-il+1,pr-1);
        
        return root;
    }
    int q[N],tt=-1,hh=0;
    int bfs(int u){
        q[++tt]=u;
        int head=hh,tail=tt;
        int step=1;
        while(hh<=tt){
            while(hh<=tail){
                int t=q[hh++];
                if(l.count(t)) q[++tt]=l[t];
                if(r.count(t)) q[++tt]=r[t];
            }
            //奇数层需要反转倒着输出
            if(step%2) reverse(q+head,q+tail+1);
            step++;
            head=hh;tail=tt;
        }
        
        cout<<q[0];
        for(int i=1;i<=tt;i++) cout<<" "<<q[i];
    }

    int main(){
        cin>>n;
        for(int i=0;i<n;i++){
            cin>>inord[i];
            pos[inord[i]]=i;
        }
        for(int i=0;i<n;i++) cin>>post[i];
        int root=build(0,n-1,0,n-1);
        
        bfs(root);
        
        return 0;
    }

    1138.Postorder Traversal (25分)(二叉树的建立)

    思路
    这一题就是在建树的过程中记录下第一个后序遍历的数字，其实建树的过程也是在对树进行一个遍历，这个遍历是根据前序序列和中序序列来的。

    代码

    Postorder Traversal
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    #include<iostream>
    #include<map>
    #include<algorithm>
    using namespace std;

    const int N = 50010;

    map<int,int> l,r,pos;
    int pre[N],inord[N],post;
    int n;
    int build(int il,int ir,int pl,int pr){
        int root=pre[pl];
        int k=pos[root];
        /*如果要求的是前序遍历的第一个数字，那么记录的位置应该放在这里*/
        if(k>il) l[root]=build(il,k-1,pl+1,pl+1+k-1-il);
        /*中序放在这里*/
        if(k<ir) r[root]=build(k+1,ir,pl+1+k-1-il+1,pr);
        
        //还没有赋值post时，即为第一个数字
        if(!post) post=root;
        return root;
    }

    int main(){
        cin>>n;
        for(int i=0;i<n;i++) cin>>pre[i];
        for(int i=0;i<n;i++){
            cin>>inord[i];
            pos[inord[i]]=i;
        }
        
        build(0,n-1,0,n-1);
        cout<<post;
        return 0;
    }

    🌞1066.Root of AVL Tree (25分)(平衡树)

    AVL知识总结

    AVL树依然是一棵二叉查找树，只不过对于AVL树的任意结点来说，其左子树与右子树的高度之差(平衡因子)的绝对值不超过1。因此如果在插入的过程中平衡因子>1了，那么我们就需要对相应结点的位置做调整。

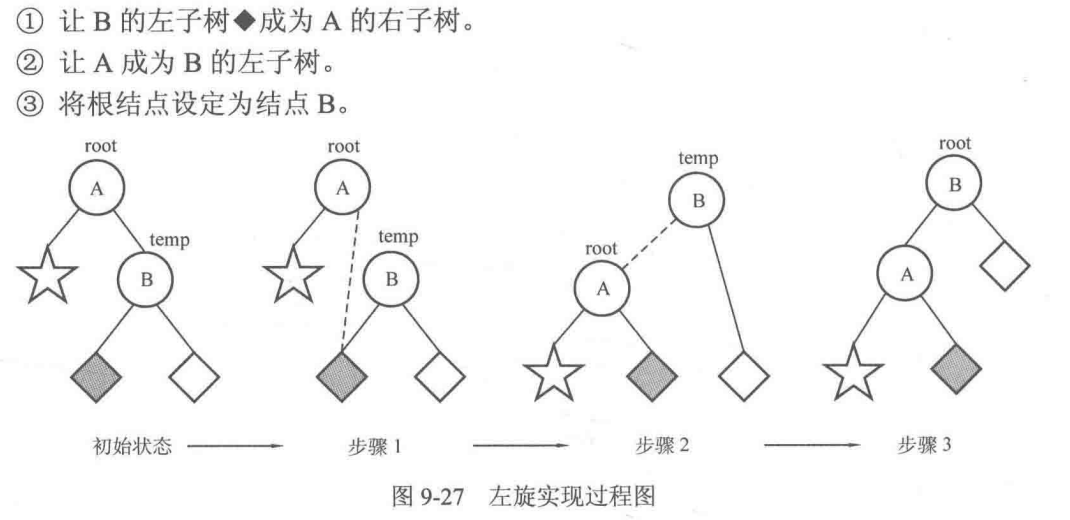
    左旋

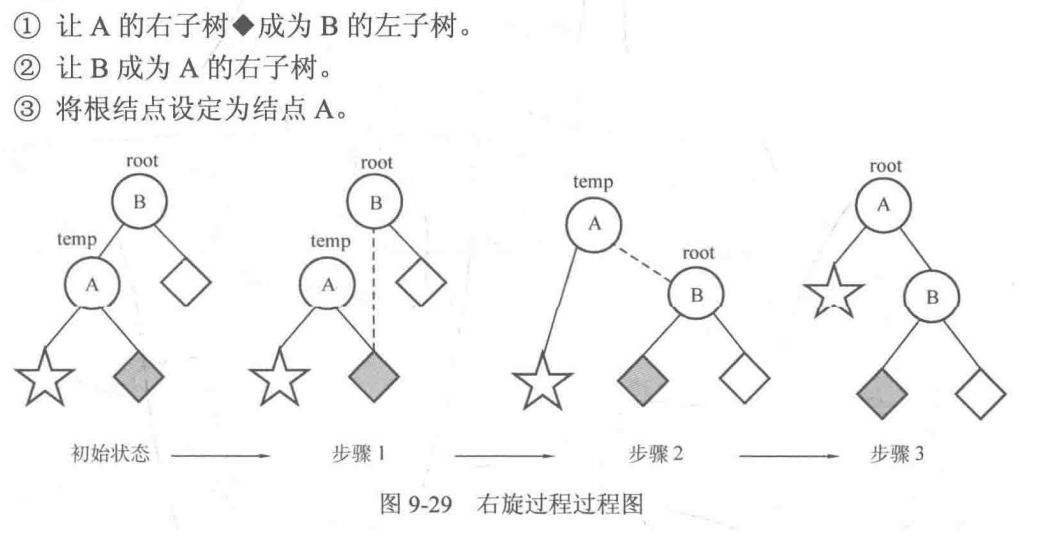
    右旋

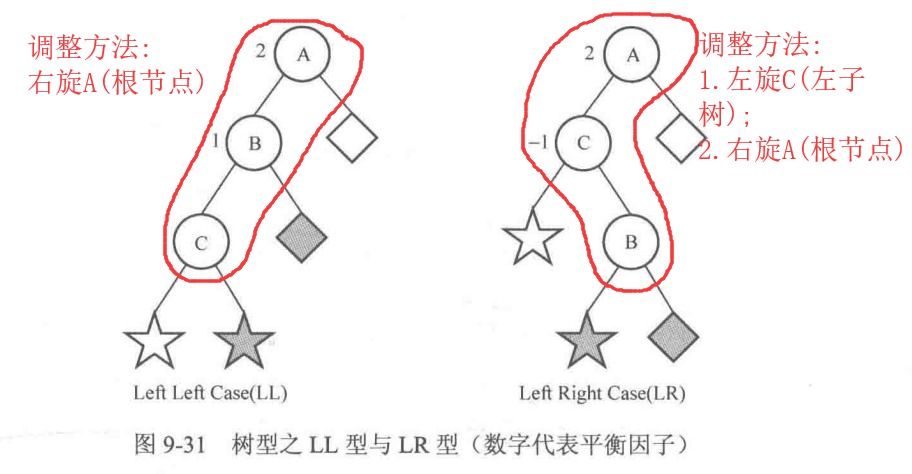
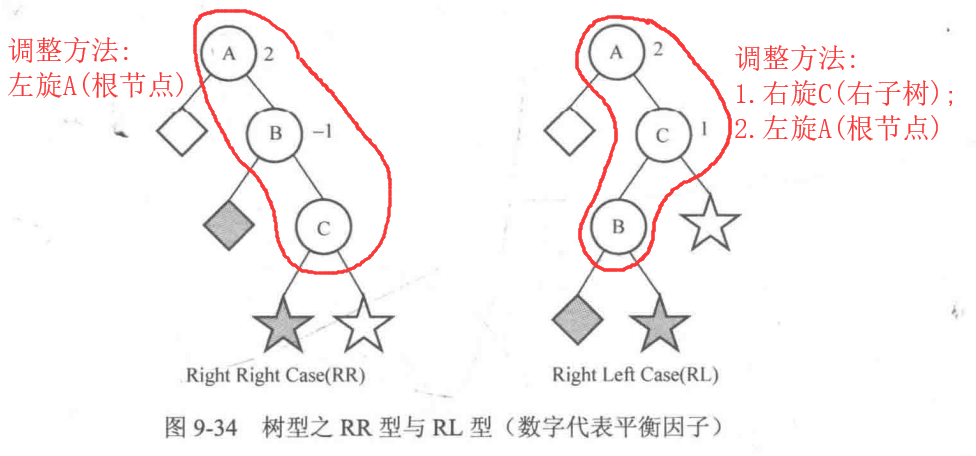
    值得注意的是平衡树的左旋和右旋只会改变平衡树的结构而不会改变这棵树的中序遍历。在知道了调整结点的方法之后，我们还需要知道在不同的情况下该怎么去调整结点。

    以下对LL,LR,RR,RL四种类型的情况进行讨论，给出了在这些情况下我们改如何去调整结点使得达到平衡。

    接下来只用按照上面的分析实现一遍即可！

    代码

    Root of AVL Tree
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    #include<iostream>

    using namespace std;

    const int N = 30;
    int l[N],r[N],w[N],h[N],idx;
    int n;
    //更新结点的高度
    void update(int u){
        h[u]=max(h[l[u]],h[r[u]])+1;
    }

    //左旋
    void L(int &u){
        int p=r[u];//把当前根节点保存下来
        r[u]=l[p];l[p]=u;
        update(u),update(p);
        u=p;//由于u加了引用，所以这里相当于是改变了根节点
    }

    //右旋
    void R(int &u){
        int p=l[u];
        l[u]=r[p];r[p]=u;
        update(u),update(p);//这个地方先跟新u(旧的根节点)还是先跟新p(新的根节点)一样，
    //在这个地方不管怎样首先保证了u是被正确更新的，
    //假如先更新了u,那么显然在这个函数中p就无法得到正确的更新，
    //但是我们在insert()函数中还会更新一次所以会纠正错误
        u=p;
    }

    //得到左右子树高度之差
    int get(int u){
        //左子树高度减去右子树高度
        return h[l[u]]-h[r[u]];
    }

    //插入结点
    void insert(int &u,int x){
        if(!u){
            u=++idx;
            w[u]=x;
        }else if(w[u]>x){
            insert(l[u],x);
            if(get(u)==2){//左子树比右子树高2,则需要调整左子树
                if(get(l[u])==1)//LL型，左子树的左边比较高
                    R(u);
                else L(l[u]),R(u);//LR型
            }
        }else{
            insert(r[u],x);
            if(get(u)==-2){
                if(get(r[u])==-1)//RR型
                    L(u);
                else R(r[u]),L(u);//RL型
            }
        }
        //插入结点后不需要左旋右旋的时候需要在这边更新一下高度
        update(u);
    }

    int main(){
        cin>>n;
        int root=0;
        while(n--){
            int x;
            cin>>x;
            insert(root,x);
        }
        
        cout<<w[root];
        
        return 0;
    }

    1123.Is It a Complete AVL Tree (30分)(AVL+完全二叉树的存储)

    思路
    这一题首先用上一题中介绍的方法建好AVL平衡树，然后我们以层序的方式遍历这棵树，记录每个节点按完全二叉树规则存到一个数组中时的下标,如果最后一个结点的下标恰好等于n那么代表这棵AVL是一个完全二叉树，否则不是。

    代码

    Is It a Complete AVL Tree 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    #include<iostream>

    using namespace std;

    const int N = 40;
    int l[N],r[N],w[N],h[N],pos[N],idx;//pos是用来记录树的每个节点按完全二叉树规则存到一个数组中时的下标
    int n;
    void update(int u){
        h[u]=max(h[l[u]],h[r[u]])+1;
    }

    void L(int &u){
        int p=r[u];
        r[u]=l[p];l[p]=u;
        update(p);update(u);
        u=p;
    }

    void R(int &u){
        int p=l[u];
        l[u]=r[p];r[p]=u;
        update(p);update(u);
        u=p;    
    }

    int get(int u){
        return h[l[u]]-h[r[u]];
    }

    void insert(int &u,int x){
        if(!u){
            u=++idx;
            w[u]=x;
        }else if(w[u]>x){
            insert(l[u],x);
            if(get(u)==2){
                if(get(l[u])==1) R(u);
                else L(l[u]),R(u);
            }
        }else{
            insert(r[u],x);
            if(get(u)==-2){
                if(get(r[u])==-1) L(u);
                else R(r[u]),L(u);
            }
        }
        update(u);
    }

    int q[N],tt=-1,hh=0;
    bool bfs(int u){
        q[++tt]=u;
        pos[u]=1;
        bool iscom=true;
        while(hh<=tt){
            int t=q[hh++];
            if(pos[t]>n) iscom=false;
            if(l[t]){
                q[++tt]=l[t];
                pos[l[t]]=2*pos[t];//以完全二叉树的方式进行存储
            } 
            if(r[t]){
                q[++tt]=r[t];
                pos[r[t]]=2*pos[t]+1;
            }
           
        }
        return iscom;
    }

    int main(){
        cin>>n;
        int root=0;
        for(int i=0;i<n;i++){
            int x;
            cin>>x;
            insert(root,x);
        }
        bool iscom=bfs(root);
        cout<<w[q[0]];
        for(int i=1;i<=tt;i++) cout<<" "<<w[q[i]]; 
        puts("");
        if(iscom) puts("YES");
        else puts("NO");
       
        return 0;
    }

    1135.Is It A Red-Black Tree (30分)(二叉树的建立)

    思路
    首先我们要先得到树的中序遍历，根据BST的性质我们知道只用把前序遍历给排序一遍即可，但是这里需要注意的是我们在保存中序遍历的元素的时候要加绝对值，因为题中给元素+符号是为了区分红色和黑色，而真正的元素大小不应该考虑符号。
    因此在得到这些中序和前序序列之后，我们只用在建树的过程中判断下该树是不是满足红黑树的性质即可。这里红黑树要满足的条件有:
  • 根是黑色的。
  • 红色结点的儿子都是黑色结点。
  • 根节点到所有叶子节点上的黑色结点的数量相同。
    • 还需要注意的一点是，这一题给的前序序列可能并不能构成一棵BST，即当在中序序列中找不到相应的根节点的时候就证明不可以构成。

    代码

    Is It A Red-Black Tree 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    #include<iostream>
    #include<algorithm>
    #include<map>
    using namespace std;

    const int N = 40;
    int pre[N],inord[N];
    map<int,int> pos;
    int n;
    bool ans=true;
    int build(int il,int ir,int pl,int pr,int &sum){
        int root=pre[pl];
        int k=pos[abs(root)];
        
        if(k<il||k>ir){
            ans=false;//可能这个输入的前序遍历并不合法,根本就够不成一颗树
            return 0;
        }
        int rootl=0,rootr=0;//0的话也是代表黑色
        int suml=0,sumr=0;
        if(k>il) rootl=build(il,k-1,pl+1,pl+1+k-1-il,suml);
        if(k<ir) rootr=build(k+1,ir,pl+1+k-1-il+1,pr,sumr);
        /*由于这里需要统计左右子树的情况，所以先递归完左右子树之后再进行红黑树条件判断*/
        if(suml!=sumr) ans=false;//1)如果左右子树的黑色结点数量不相同则为false  
        sum=suml;//记录下子树的结点数量
        if(root<0){//红色结点
            if(rootl<0||rootr<0) ans=false;//2)如果红色结点的儿子存在红色儿子则为false
            //这里值得注意的是，之所以上面的rootl和rootr初始化为0，就是为了当当前的根节点root没有
            //左孩子或者右孩子的时候保证NULL节点是黑的
        }else sum++;//黑色结点的话则沿途的黑色结点数量+1
        
        return root;
    }

    int main(){
        int T;
        cin>>T;
        while(T--){
            cin>>n;
            for(int i=0;i<n;i++){
                cin>>pre[i];
                inord[i]=abs(pre[i]);//负号只是为了区分红色和黑色的，所以要想sort得到正常的值这里应该abs
            }
            sort(inord,inord+n);
            pos.clear();
            ans=true;//多个测试用例，记得把这些重复使用的变量恢复原状
            for(int i=0;i<n;i++) pos[inord[i]]=i;
            int sum=0;
            int root = build(0,n-1,0,n-1,sum);
            //3)根节点为红色则为负数
            if(root<0) ans=false;
            if(ans) puts("Yes");
            else puts("No");
        }
        
        return 0;
    }

    1053.Path of Equal Weight (30分)(DFS)

    思路
    这里主要就是dfs遍历一棵树,然后记录下沿途所有结点权值，把权值和==目标值s的路径保存下来，之后输出即可。这里需要注意的是对于vector<int>类型的变量在sort的时候会自动的排序，而不用我们自己写什么cmp函数之类的东西。

    代码

    Path of Equal Weight
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    #include<iostream>
    #include<algorithm>
    #include<cstring>
    #include<vector>
    using namespace std;

    const int N = 110;
    int h[N],e[N],ne[N],w[N],idx;//注意这里的w是单个结点的权重
    int n,m,s;
    vector<vector<int>> ans;

    void add(int a,int b){
        e[idx]=b;ne[idx]=h[a];h[a]=idx++;
    }

    void dfs(int u,int sum,vector<int> &path){//根节点；路径上权值之和；路径
        if(~h[u]==0)
            if(sum==s) ans.push_back(path);
        for(int i=h[u];~i;i=ne[i]){
            int j=e[i];
            path.push_back(w[j]);
            dfs(j,sum+w[j],path);
            path.pop_back();
        }
    }

    int main(){
        cin>>n>>m>>s;
        for(int i=0;i<n;i++) cin>>w[i];
        memset(h,-1,sizeof h);
        while(m--){
            int id,k;
            cin>>id>>k;
            while(k--){
                int t;
                cin>>t;
                add(id,t);
            }
        }
        vector<int> path;
        path.push_back(w[0]);//0号点是根节点
        dfs(0,w[0],path);
        
        sort(ans.begin(),ans.end(),greater<vector<int>>());//这里要按造降序进行排列
        for(auto p:ans){
            cout<<p[0];
            for(int i=1;i<p.size();i++) cout<<" "<<p[i];
            puts("");
        }    
        
        return 0;
    }

    1094.The Largest Generation (25分)(层序遍历)

    思路
    这一题就是层序遍历一下树，然后统计下每层的结点数量，记录最大的一层，输出数量和第几层即可。
    The Largest Generation 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    #include<iostream>
    #include<cstring>
    using namespace std;

    const int N = 110;
    int h[N],e[N],ne[N],idx;
    int m,n;
    void add(int a,int b){
        e[idx]=b;ne[idx]=h[a];h[a]=idx++;
    }

    int q[N],tt=-1,hh=0;
    int max_pop,max_depth;
    void bfs(int u){
        q[++tt]=u;
        int depth=0;
        int head=hh,tail=tt;
        while(hh<=tt){
            depth++;
            int cnt=tail-head+1;
            if(cnt>max_pop){
                max_pop=cnt;
                max_depth=depth;
            }
            //由于这里是一棵树，点是不会重复的入队的
            while(hh<=tail){
                int t=q[hh++];
                for(int i=h[t];~i;i=ne[i]){
                    int j=e[i];
                    q[++tt]=j;
                }
            }
            head=hh;tail=tt;
        }
    }

    int main(){
        cin>>n>>m;
        memset(h,-1,sizeof h);
        while(m--){
            int id,k;
            cin>>id>>k;
            while(k--){
                int t;
                cin>>t;
                add(id,t);
            }
        }
        bfs(1);
        cout<<max_pop<<" "<<max_depth;
        return 0;
    }
    #

    喜欢这篇文章？打赏一下作者吧

    评论

    最新文章

    ×