2021-01-04计算机图形学 0次访问

切线空间与法线贴图

详解切线空间与法线贴图🧨🧨🧨

法线贴图

法线贴图中存储的是每个片元（fragment）的法线。

使用法线贴图

我们在片元着色器中采样法线贴图获取每个片元的法线。法线贴图是一张图片，其中保存的是rgb的颜色信息，rgb的范围是0到1，但是法线是一个三维向量，每个分量的范围是-1到1，因此对于采样得到的法线我们要把它映射回-1到1的范围。

使用法线贴图，OpenGL伪代码

uniform sampler2D normalMap;  

void main()
{           
    // 从法线贴图范围[0,1]获取法线
    normal = texture(normalMap, fs_in.TexCoords).rgb;
    // 将法线向量转换为范围[-1,1]
    normal = normalize(normal * 2.0 - 1.0);   

    [...]
    // 像往常那样处理光照
}

切线空间

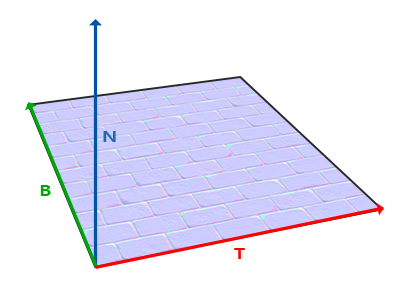
法线贴图中的法线向量定义在切线空间中。
切线空间的x,y,z轴分别对应于切线向量（T），副切线相量（B）和法线向量（N）。其中切线向量和副切线向量与纹理坐标的U和V方向对齐。法线向量即三角形表面的法线向量，三个向量两两垂直。
由于三角形平面的法线向量做了z轴，因此大多片元的法线向量都偏向z轴(0,0,1)，由于切线空间坐标的范围是-1到1，而颜色的范围是0到1，因此映射到0到1的范围时，(0,0,1)就会转换为(0.5,0.5,1)（可以在调色板上试一下这种颜色长什么样子！），所以整张图片看起来是偏蓝的，可能偶尔有几个凹凸不平的地方对应的片元的法线偏离了三角形的法线，向着x,y轴偏了一下，因此图片中也有少数的地方泛紫或泛绿。

计算TBN矩阵

在上面关于法线贴图的讨论中，我们已经得到了切线空间下的法线向量，那么该如何使用它们呢？这就和TBN矩阵密不可分了！
TBN这三个字母分别代表tangent、bitangent和normal向量。这是建构TBN矩阵所需的向量，因此要求TBN矩阵即求得这三个向量即可。
法一：
以下的方法是LearnOpenGL中介绍的方法，该方法利用一个三角形的顶点和纹理坐标（纹理坐标和切线向量在同一空间中）计算出切线和副切线（PS：顶点的法向N已知）。

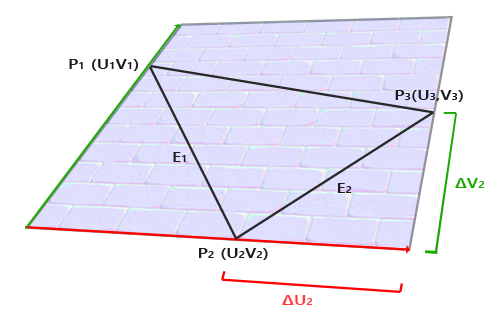
从图中可以看到法线贴图的切线和副切线与纹理坐标的两个方向对齐。图中边E2与纹理坐标的差ΔU2、ΔV2构成一个三角形。ΔU2与切线向量T方向相同，而ΔV2与副切线向量B方向相同。这也就是说，所以我们可以将三角形的边E1与E2写成切线向量T和副切线向量B的线性组合：
$$E_1 = \Delta U_1T + \Delta V_1B$$$$E_2 = \Delta U_2T + \Delta V_2B$$我们也可以写成这样：
$$(E_{1x}, E_{1y}, E_{1z}) = \Delta U_1(T_x, T_y, T_z) + \Delta V_1(B_x, B_y, B_z)$$$$(E_{2x}, E_{2y}, E_{2z}) = \Delta U_2(T_x, T_y, T_z) + \Delta V_2(B_x, B_y, B_z)$$E 是两个向量位置的差，ΔU和ΔV是纹理坐标的差。然后我们得到两个未知数（切线T和副切线B）和两个等式。上面的方程允许我们把它们写成另一种格式：矩阵乘法
$$\begin{pmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{pmatrix} = \begin{pmatrix} \Delta U_1 & \Delta V_1 \\ \Delta U_2 & \Delta V_2 \end{pmatrix} \begin{pmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{pmatrix}$$因此这样可以解出T和B了：$$\begin{pmatrix} \Delta U_1 & \Delta V_1 \\ \Delta U_2 & \Delta V_2 \end{pmatrix}^{-1} \begin{pmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{pmatrix} = \begin{pmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{pmatrix}$$计算T和B的逆矩阵很简单，这里直接是伴随矩阵求逆法，即首先求伴随矩阵，二维矩阵的伴随矩阵即“主对换副变号”口算可得，然后用伴随矩阵除其行列式即为逆矩阵：$$\begin{pmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \end{pmatrix} = \frac{1}{\Delta U_1 \Delta V_2 - \Delta U_2 \Delta V_1} \begin{pmatrix} \Delta V_2 & -\Delta V_1 \\ -\Delta U_2 & \Delta U_1 \end{pmatrix} \begin{pmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{pmatrix}$$有了最后这个等式，我们就可以用公式、三角形的两条边以及纹理坐标计算出切线向量T和副切线B。
法二：（常用）
对于上面的做法其实duck不必，一般情况下我们是知道法线信息和切线信息的，这样我们可以直接根据二者叉乘得到副切线，然后按照T、B、N的顺序按列排列成一个矩阵即得到了TBN矩阵。

TBN矩阵是怎么来的？

使用TBN矩阵可以把切线坐标空间的向量转换到世界坐标空间（当然也可以是别的空间，例如模型空间，这具体和你用什么空间下的向量来组成TBN矩阵有关）。
根据坐标空间的转换关系可知，每个坐标空间都是另一个坐标空间的子空间，坐标空间的变换实际上就是在父空间和子空间之间做转换。如果坐标转换矩阵是正交矩阵（转置矩阵和逆矩阵相同），【已知子坐标系三个坐标轴在父坐标系下的表示xyz（此时子坐标转换为父坐标的矩阵是很显然可以求得的，而父坐标到子坐标的转换矩阵需要求该矩阵的逆矩阵得到）】那么父坐标系到子坐标系中向量的转换矩阵则是xyz按行排列的矩阵，而子坐标系转换到父坐标系则是xyz按列排列的矩阵。
以从切线空间转换到世界空间为例。其中T,B,N分别是切线空间三个坐标轴在世界空间下的表示。那么切线空间就是子空间，而世界空间是父空间，因此把切线空间中的向量转换到世界空间就相当于是子空间向父空间转换，因此把T,B,N按列排列所得的矩阵就是切线空间到世界空间的转换矩阵。
【PS1】父坐标到子坐标的转换就是把用父坐标表示的点和矢量用子坐标表示。子坐标到父坐的转换就是把子坐标表示的点和矢量用父坐标表示。
【PS2】切线空间到模型空间的变换仅会存在旋转和缩放变换（因为是对方向矢量进行变换，因此平移变换在这里可以不用考虑），旋转矩阵是正交矩阵，但缩放矩阵并不是。如果只存在统一缩放，那么我们仍然可以以目前所描述的方法直接使用转置矩阵（此时转置矩阵和逆矩阵之间的差别只在于差了一个统一缩放的系数），我们只需要把最后的结果归一化就可以抵消统一缩放的影响。但如果存在非统一缩放，那么我们就不能直接使用转置矩阵来作为逆矩阵了。
【PS3】由于TBN矩阵的变换只涉及缩放和旋转，因此它是一个线性变换。

使用TBN矩阵

我们直接使用TBN矩阵，这个矩阵可以把切线坐标空间的向量转换到世界坐标空间（此时TBN也要在世界坐标空间下，即在构造TBN矩阵的时候把三个向量转换到世界坐标下，当然这里值得注意的是，如果要保证精确性，那么在转换法线向量的时候要注意“法线变换”的问题，见《unity shader入门精要》4.7节）。因此我们把它传给片段着色器中，把通过采样得到的法线坐标左乘上TBN矩阵，转换到世界坐标空间中，这样所有法线和其他光照变量就在同一个坐标系中了。
我们也可以使用TBN矩阵的逆矩阵，这个矩阵可以把世界坐标空间的向量转换到切线坐标空间。因此我们使用这个矩阵左乘其他光照变量，把他们转换到切线空间，这样法线和其他光照变量再一次在一个坐标系中了。
我们在顶点着色器中构造TBN矩阵（根据三角形的一个顶点即可算出该三角形的TBN矩阵，该顶点的法线和切线易得，很快就可以算出TBN矩阵），之后传入片元着色器，在片元着色器中，同一个三角形内的片元属于同一个切线空间，同一个三角形内共同使用一个TBN矩阵，然后用采样得到的法线乘TBN矩阵就可以得到该片元在世界坐标系下的法线向量。

参考：learnopengl

#计算机图形学